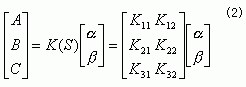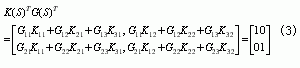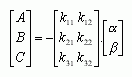引言
    为保证平台稳定，被调平台有五条支腿，分别用5个执行元件控制其高度，以调整平台的水平度;用2个水平敏感元件检测其水平度，2个水平敏感元件垂直安装，分别用于检测平台前后方向的水平度和检测平台左右方向的水平度。图1是被调平台与支腿和水平传感器安装示意图(图中未标出平台上的设备)。

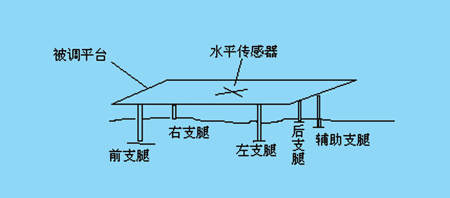
图1   被调平台与支腿和水平传感器安装示意图

5个调平支腿高度及2个水平敏感元件的输出，构成了五输入二输出的多输入输出系统，每一调平支腿高度变动，都有可能影响平台的水平度，因此它是一个强耦合的系统。

2  完全解耦的控制方法
    系统虽有5个输入，2个输出，但我们知道，三点决定平面，所以在调平控制量中有二个输入量是冗余量，只需选择平台重心在三支点构成的三角形内，控制这个三角形的三个支腿高度，即可实现调平;在调平结束后，再控制其余二个支腿着地即可。所以实际系统应是三输入二输出系统，经过分析可以得到水平敏感元件的输出α与β是三个调平支腿高A、B与C的函数:
     α=f1(A，B，C)
     β=f2(A，B，C)
平台调平后，应得到α≤δ，β≤δ。δ是一个允许的很小倾角。A、B、C与α、β之间是强耦合的。
应用理论和实验方法都可得出其传递函数，设平台输入与输出关系表示如下: 

式中GNM是α、β对于A、B、C的传函;GNM中下标N=1、2代表水平敏感元件的输出α与β，M=1、2、3代表三支腿高A、B与C。设有一个预补偿矩阵Kp(s)使(2)式成立。

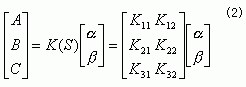
    式中KPQ中下标Q=1、2代表预补偿函数的二个输入α与β，P=1、2、3代表补偿传函的三个输出A、B与C。若

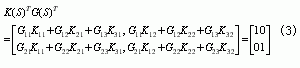
    则可实现完全解耦。为使完全解耦，必需求出k(S)，并且按(4)式实时计算A、B和C，然后实施控制。

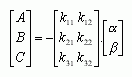
由(3)式解出k(S)，代入(4)式并离散化(4)式，用计算机实时地计算出控制量A、B、C，就构成了快速自动调平系统。然而k(S)不容易显式解得，(4)式的实时计算量大;以及当用伺服系统控制调平支腿的高度时，最少要有测量3个支腿高度的传感器和两个测量平台水平度的传感器，硬件电路相对复杂，开发时间长;这些因素都限制了完全解耦控制方法的使用。|
3  剔除冗余量的解耦控制方法
某些平台上的设备运行中不需实时调平，只要求开始工作前进行一次调平，对调平过程速度要求也不高。这种平台的调平方法，可用剔除冗余量的解耦控制方法;将调平过程分两步进行，首先调平某个倾角使之达到水平要求之后，将其锁定，然后再去调另外一个倾角。在第一步时，剔除了一个倾角及两个支腿的高，使控制系统变成了单入单出控制系统。第二步剔除已调平了的倾角及相应的已完成调平任务的两个支腿。这样第二步调平也变成了单入单出控制系统。这种做法是一种剔除冗余量的解耦控制方法。
    具体调平过程叙述如下:首先选择平台重心所在三支腿构成的三角形中的三个支腿;在平台未调平前，三个支腿连结成的三角形中，必有一条边的倾角最大，这条边是由最高与最低两支点的连线，与它平行的(或夹角最小的)水平敏感元件的输出最大，也即由此水平传感器测出的倾角最大，以此水平敏感元件的输出作被控量，以高度最低支腿的高为控制量，构成单入单出的闭环控制系统。这时，虽然调整最低位置支腿高时，会同时影响两个倾角，但未被选用的水平传感器的倾角变化可在第二步时再调平，因此在第一步调平过程中，最高和次高支腿高作为冗余量被暂时剔除了，较小的倾角的输出也作为冗余量被剔除了。第一步调平过程，直至此最大倾角被调平为止。当此倾角调平后，以此水平线为轴，平台便成了“跷跷板”，在平台重心作用下，原次高支腿变成了新的最低支腿。原倾角较小的传感器输出变成最大。